
This is simply the highest non-outlier value in the dataset being visualized by the box plot. It is often said to be a better measure of spread when compared to the range. The interquartile range is the difference between the first quartile and the third quartile. For example, the first quartile of 100 is (¼)*100*3= 75. It is calculated by multiplying the one-fourth of the value by 3. The third quartile is also known as the upper quartile because it is calculated at the 75th percentile. For example, the first quartile of 100 is (¼)*100*1= 25. It is calculated by multiplying the one-fourth of the value by 1. The first quartile is also known as the lower quartile because it is calculated at the 25th percentile. The median is also known as the second quartile. However, when it is even, the median is calculated by finding the average of the two numbers in the middle. The median can be easily formulated when the dataset contains an odd number of values. The median is the quantity that falls in the middle when a set of values are arranged in an ascending or descending order. Although rare, some box plots do not have whiskers. The boxes can either be drawn vertically or horizontally depending on the goal of visualizing the data. That is, the rectangular bars(or boxes), top of the boxes indicating the upper quartile, the bottom of the boxes indicating the lower quartile, the centerline indicating the margin, and the line drawn from each end of the boxes is known as the whisker. The name, box and whisker plot is derived from the nature of the graph. It may also have line extensions extending from the boxes, which usually indicates variability beyond the upper and lower quartiles. Box Plot DefinitionĪ box plot is a statistical data visualization technique that uses rectangular bars to indicate data groups through their quartiles. There are different steps involved in this process, and it will be further explained in the rest of this article. Box & Whisker plots make use of the five-way summary (median, lower quartile, higher quartile, minimum, and maximum) when describing data. Some other methods that require calculation include a histogram, which needs a class interval and a pie chart that requires one to calculate the degree of each slice in the pie.Ĭomputations are no doubt a common occurrence in statistical analysis, but minimal when visualizing data. Again, you can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.Box & Whisker plot is one of the few data visualization techniques that perform further computations on the dataset before it can be visualized. This makes sense, the median is the average of the middle two numbers.Ħ.

You can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.ĥ.

In this example, n = 8 (number of data points).Ĥ. This function interpolates between two values to calculate a quartile. For example, select the even number of data points below.Įxplanation: Excel uses the QUARTILE.EXC function to calculate the 1st quartile (Q 1), 2nd quartile (Q 2 or median) and 3rd quartile (Q 3). Most of the time, you can cannot easily determine the 1st quartile and 3rd quartile without performing calculations.ġ. As a result, the whiskers extend to the minimum value (2) and maximum value (34). As a result, the top whisker extends to the largest value (18) within this range.Įxplanation: all data points are between -17.5 and 34.5. Therefore, in this example, 35 is considered an outlier.
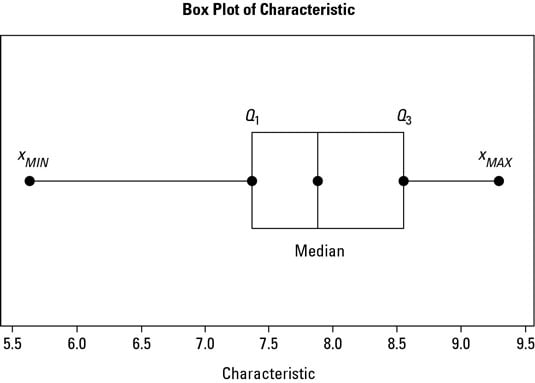
A data point is considered an outlier if it exceeds a distance of 1.5 times the IQR below the 1st quartile (Q 1 - 1.5 * IQR = 2 - 1.5 * 13 = -17.5) or 1.5 times the IQR above the 3rd quartile (Q 3 + 1.5 * IQR = 15 + 1.5 * 13 = 34.5). In this example, IQR = Q 3 - Q 1 = 15 - 2 = 13. Q 3 = 15.Įxplanation: the interquartile range (IQR) is defined as the distance between the 1st quartile and the 3rd quartile. The 3rd quartile (Q 3) is the median of the second half. The 1st quartile (Q 1) is the median of the first half. The median divides the data set into a bottom half. The x in the box represents the mean (also 8 in this example). On the Insert tab, in the Charts group, click the Statistic Chart symbol.Įxplanation: the middle line of the box represents the median or middle number (8).


 0 kommentar(er)
0 kommentar(er)
